With ever-growing possibilities and interconnectivity on the internet, we rely more and more on it being secure. However, our classical internet is not provably secure, could a quantum internet solve our problems?
Whenever there is a need to send messages that cannot be read by adversaries, there is a need for encryption since any message may be intercepted and read out. Throughout history, the possibility of sending secure messages has always been of great importance. Whether it was to notify your troops that the enemy was engaging, or sending messages between diplomats and their home governments. It has always been important to send messages that other people cannot read.
Cryptography is the procedure of encrypting and decrypting messages such that secure communication between two parties is possible. Current cryptographic protocols rely on the idea that there are certain tasks that are difficult for computers. It is a very interesting feat that with these ideas it is possible to send messages between two parties on the internet securely without the need for them to meet prior.
The ancient Greeks used the Polybius square, where letters are decoded as the coordinates of a square with inscribed letters. The Romans used Caesar ciphers, in which letters are shifted in the alphabet with some key. And during the Second World War, the Germans used the Enigma machine, which relied on extremely intricate internal mechanics to create codes. Over time these methods, when implemented correctly, became increasingly difficult to break. While Caesar codes have a possible attack of counting the most frequent letters, and comparing this to the frequency of letters in the language, the Enigma machine relied on mechanical principles to generate a cipher, and trying to decode messages was incredibly difficult.
However, security in all these examples relies on some sort of predetermined strategy. In other words, it required the people who wish to communicate to meet before and discuss some strategy and share a secret. With Caesar codes, the receiving party needed to know the cipher the sending party used, and with the Enigma, one needed a full machine to decrypt the message. This seems intuitive, if two parties want to send each other a message that cannot be read by anyone who intercepts their messages, one might think that they need some extra resource to use. Remarkably, it turns out that it is possible to securely send messages between each other, given that some mathematical problems are hard to solve for computers, and is used by you probably every day. This procedure is known as public-key cryptography.
The most widely used public-key cryptography scheme is RSA (named after Rivest, Shamir, and Adleman who described the algorithm in 1977). In this scheme, there is a public encryption key and a private decryption key. Suppose some person (Alice) wants to send a message to someone else (Bob). To do so Bob creates an encryption and decryption key and sends Alice the encryption key, with this key Alice encrypts her message and sends it to Bob. Finally, only Bob can decrypt this message since only he holds the decryption key.
The security of this scheme depends on the hardness of factoring a product of two prime numbers. Here hard means that there is no efficient algorithm for a computer to find back the two prime numbers out of the product of these two primes. While there are efficient algorithms for computers to find two prime numbers and multiply them with each other. Thus, Alice and Bob may send each other messages securely without sharing everything prior.
However, there are two problems with the RSA protocol described above. While we don’t have any efficient algorithms to do factoring on a classical computer it will be possible to efficiently factorize large numbers on a quantum computer using Shor’s Algorithm, named after Peter Shor who published the algorithm in 1994.
Yet, while quantum computers attack our current most implemented methods of encryption, they also open the door to new methods of encryption that actually use quantum effects. There are protocols that use quantum effects, which can be shown to be information-theoretically secure. One of these is the BB84 algorithm, named after its discoverers Bennet and Brassard. In this protocol we need to send quantum messages over some form of a quantum communication network. Thus, while quantum computers attack our current most implemented methods of encryption, it also opens the door to new methods of encryption that actually use quantum effects.
Secondly, when Bob receives a message from Alice he needs to be sure that it actually originated from Alice. The security of RSA, as well as BB84, depends on the existence of an authenticated public classical channel. Here authenticated means that we know with certainty where the messages were sent from, and public means that the message is public for everyone. A reason this property is needed is to prevent an attack called a man-in-the-middle (mitm) attack.
In a mitm-attack, a third party places themself between two parties who think they are talking to each other, intercepts all messages, and sends those of their own. For example, in the RSA encryption scheme, they simply send their own encryption key to Alice and block the encryption key of Bob. Then Alice encrypts her message using this malicious key, and the person in the middle can read the message Alice sends.
To try to secure us against this problem, it could be that quantum effects will again allow us to protect ourselves against mitm-attacks on a quantum internet. A possible way to authenticate a channel and make sure its connection is with the right person is to verify that the other person is at the geographical location you expect them to be. In other words, we use the position of somebody to protect us against attacks from some different position, i.e. a person in the middle. This is the task of position verification protocols.
Consider the following simplified setting in one dimension (instead of the 3 dimensions we normally live in), where two verifiers are placed on a line with a prover in the middle. The task for the verifiers is to confirm the position of the prover in the middle. They can do this by sending a message from both sides with the speed of light, and asking a prover to reply immediately and send their message with the speed of light. Then, checking whether the prover answers on time, the two verifiers can confirm that the prover is at their claimed location.
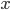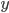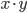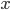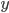For example, they could send a bit from the one side, and a bit from the other and ask the prover to answer the product of the two . The idea is that this can only be answered if a person holds both and , by the speed of light the only position in space where a prover can answer on time is at their prescribed location.
However, this protocol can be attacked by two colluding adversaries who are placed between the verifiers and the prover. They simply intercept both messages and forward them to each other, such that after communicating they both hold 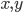and can calculate the product of the two. This way they fool the verifiers.
Figure 1: Schematic drawing of two verifiers on a line and a prover in the middle, with colluding attackers between the prover and the verifiers.
It has even been shown that it is impossible to securely do position verification when the messages of the verifiers are classical, this is because classical communication can always be copied by colluding attackers between the verifiers.
However, again there is a possible use for the quantum internet. It is a fundamental fact that quantum information cannot be cloned. That is, there is no general operation that takes some quantum input and outputs this quantum information twice. This is because every quantum operation must be reversible and linear, which is a fundamental property that nature implies on our quantum systems. And copying something is not a reversible operation in this setting.
In fact, by letting the verifiers send quantum information and asking for some measurement on these inputs by the prover, we can prove that there exist quantum position verification protocols that have some form of security against a coalition of colluding attackers. This proof uses the fact that quantum information cannot be simply cloned and copied between two attackers. Attackers, therefore, have to immediately measure their quantum systems which does not allow them to learn enough information about their inputs, as an honest prover who holds both would learn.
In conclusion, a lot of cryptography used on the internet relies on the property that certain tasks are difficult for computers. It turned out that some of these problems that we suspect to be difficult for classical computers are easy for quantum computers, which compromises the security of the internet. However, quantum computing allows us to use quantum effects to build cryptographic protocols that are provably safe and don’t rely on anything. Now that quantum computers are getting larger every year, the time is coming to prepare us.
In times of war, secure communication can be the difference between life and death, or even winning or losing a war. The first to patent a rotor machine in Europe was Arthur Scherbius in 1918. Scherbius’ version of the rotor machine became a commercial success, unlike the other patented machines. Scherbius named his machine Enigma.
The story goes as follows, during the last couple of decades many scientists, universities, and tech giants like IBM, Microsoft, and Google have invested largely in building this advanced machine called a quantum computer. Such a computer will be able to perform quantum computations, which rely on qubits instead of ordinary bits. The major challenge when you want to use such a qubit is that it is very unstable, and stable qubits are essential to have a proper quantum computer.
QuTech at the Delft University of Technology and TNO, in collaboration with the European Quantum Internet Alliance, are leading the efforts to establish a quantum Internet and aims at having a proof of concept version, between the cities of Amsterdam, Leiden, Delft and the Hague.
László Lovász and Avi Wigderson received the prize for their pioneering contributions to theoretical computer science and discrete mathematics. One of these contributions was the incorporation of theoretical computer science and discrete mathematics as central parts of modern mathematics.
from the one side, and a bit 
from the other and ask the prover to answer the product of the two 
. The idea is that this can only be answered if a person holds both 
and can calculate the product of the two. This way they fool the verifiers.
