Don't be intimidated by the large numbers in this article, they look intimidating but after reading this article you will see they are just numbers!
Numbers are just amazing, as a child numbers are one the first things you learn. You try to count as far as possible, the first goal is to reach 10, then 20, then 50, finally you reach 100. At some point you realize you can keep going further and further, since adding one more zero results in an even larger number. I have seen in Twitter hundreds of messages about numbers that just look wonderful. Two examples that I saw recently.
Example 1: Start with 82 and go backwards to 1. This gives the number
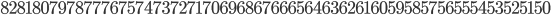
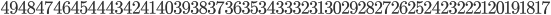
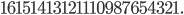
This number is a prime number!
Example 2: Consider the number 13532385396179. This number can be written as the following product
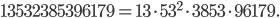
Do you see the similarity between the two parts? When I saw these tweets I was fascinated and started looking for other almost mythical numbers. How I went on searching for such numbers? Using my computer and some basic programming in Python. In this series of articles I want to show you some of my findings.
Before I can show what I found I need to tell you something about a very special kind of numbers, prime numbers. Prime numbers are numbers that can be divided only by themselves and 1. Examples of prime numbers are
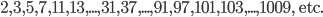
There are infinitely many prime numbers, this is a result proved by Euclides. Prime numbers are extremely useful, they are the building blocks of all the other numbers. This is because each number can be factorized into a product of prime numbers in a unique way! For example the number  can be written as
can be written as 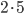 , the number
, the number 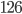 as
as 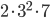 and the number
and the number 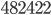 as
as 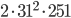 . Numbers that are not prime are called composite numbers.
. Numbers that are not prime are called composite numbers.
As I said before, I am going to explore the realm of numbers using the computational power of my computer. I am going to search for exotic prime numbers and composite numbers with some funny property. First of all, how large numbers do you think my laptop can handle (an ordinary HP)? Lets see, when I want to discuss how large numbers can get I always google the number of atoms in the universe, the result reads
It is estimated that there are between 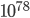 to
to 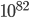 atoms in the known, observable universe. In layman's terms, that works out to between ten quadrillion vigintillion and one-hundred thousand quadrillion vigintillion atoms.
atoms in the known, observable universe. In layman's terms, that works out to between ten quadrillion vigintillion and one-hundred thousand quadrillion vigintillion atoms.
Believe me or not 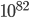 is a number your laptop can easily handle! For example in less than one second my computer computes that the two closest prime numbers to
is a number your laptop can easily handle! For example in less than one second my computer computes that the two closest prime numbers to 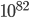 are
are
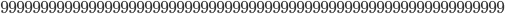
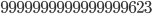
and
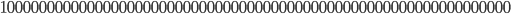
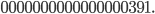
Wouldn't it by the way be mind-blowing if the exact number of atoms in the universe, which is a number between 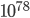 and
and 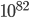 would be a prime number? What is the probability of this event? To estimate this we need to find how many primes numbers there are between
would be a prime number? What is the probability of this event? To estimate this we need to find how many primes numbers there are between 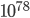 and
and 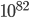 . Although I can let my computer do the work (which will take quite a while I think) I can use a mathematical theorem from number theory to give you an estimate. The Prime Number Theorem says that
. Although I can let my computer do the work (which will take quite a while I think) I can use a mathematical theorem from number theory to give you an estimate. The Prime Number Theorem says that
the number of prime numbers smaller than 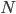 is approximately equal to
is approximately equal to 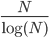 .
.
This means that between 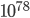 and
and 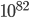 there are approximately
there are approximately
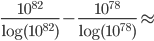
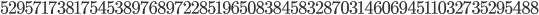
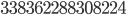
prime numbers. If we translate this to a percentage we get that 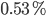 of all numbers between
of all numbers between 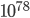 and
and 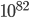 are prime numbers. This probability is a rather low number but in the end we are talking of the total number of atoms in the universe.
are prime numbers. This probability is a rather low number but in the end we are talking of the total number of atoms in the universe.
Lets go back to my exotic prime numbers. I started by looking for prime numbers consisting of only one number, such numbers are 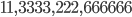 or
or 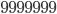 . For such a number to be prime the only candidate digit to examine is 1, since every other number will be divisible by the number of which it consists. For example
. For such a number to be prime the only candidate digit to examine is 1, since every other number will be divisible by the number of which it consists. For example  is always divisible by
is always divisible by 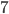 . So is there a number consisting of only 1's and also being prime? Of course you have
. So is there a number consisting of only 1's and also being prime? Of course you have 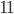 which is prime. Using a simple code in SageMath the following numbers popped out:
which is prime. Using a simple code in SageMath the following numbers popped out:
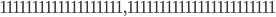
and
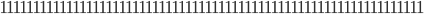
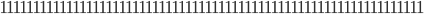
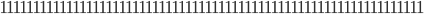
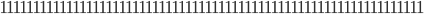
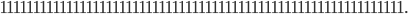
These numbers consist of 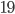 ,
, 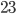 and
and 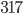 digits respectively. And all three of them are prime numbers! You will now wonder if you can make an even larger number of this type that is prime. In the program SageMath I checked even larger numbers of this kind, up to the insanely large number consisting of 1018 ones and didn't find any more primes among them. The question will unfortunately stay unanswered for now. Maybe there is one maybe not.
digits respectively. And all three of them are prime numbers! You will now wonder if you can make an even larger number of this type that is prime. In the program SageMath I checked even larger numbers of this kind, up to the insanely large number consisting of 1018 ones and didn't find any more primes among them. The question will unfortunately stay unanswered for now. Maybe there is one maybe not.
Lets venture into another funny case, I am going to search for prime numbers where you have a repeating pattern, for example 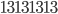 where
where 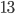 repeats for a number of times, other examples are
repeats for a number of times, other examples are 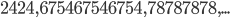 . It turns out that such a number can not be prime, it is always divisible by the smaller number that repeats to make this larger number. For example
. It turns out that such a number can not be prime, it is always divisible by the smaller number that repeats to make this larger number. For example 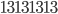 is divisible by
is divisible by 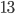 and
and 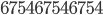 is divisible by
is divisible by 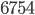 , in a follow up article I will discuss why this is the case. But you can tweak the number a little bit, say that I consider numbers of this kind, but also add an extra number in front of it, for example instead of considering
, in a follow up article I will discuss why this is the case. But you can tweak the number a little bit, say that I consider numbers of this kind, but also add an extra number in front of it, for example instead of considering 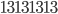 we will look for primes of the form
we will look for primes of the form 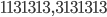 or
or 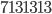 . It turns out that you can find a lot of such prime numbers! Lets see some below. The numbers
. It turns out that you can find a lot of such prime numbers! Lets see some below. The numbers
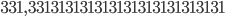
and
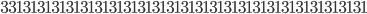
are all three prime numbers! Also the following three numbers
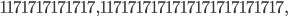
and
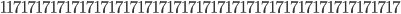
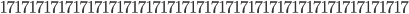
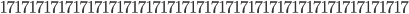
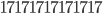
are all prime numbers. What is amazing is that if you just add one more 1 at the end then the number is no longer prime. The third number for example will become 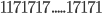 which is not a prime number. In the follow up articles I will show some more numbers with funny properties. In this article, as well as in most of the Tweets and messages on the Internet, we have seen numbers with exotic properties. But, as we will discuss in the next articles, you cannot find numbers satisfying any property you come up with. There are some things that are impossible, to show that no numbers can satisfy a property we need more than a computer, we need a mathematical argument. Wait until my next article! Of course if you have suggestions and ideas of nice properties to try out let me know and I will try to find numbers satisfying them!
which is not a prime number. In the follow up articles I will show some more numbers with funny properties. In this article, as well as in most of the Tweets and messages on the Internet, we have seen numbers with exotic properties. But, as we will discuss in the next articles, you cannot find numbers satisfying any property you come up with. There are some things that are impossible, to show that no numbers can satisfy a property we need more than a computer, we need a mathematical argument. Wait until my next article! Of course if you have suggestions and ideas of nice properties to try out let me know and I will try to find numbers satisfying them!