The Netherlands Forensic Institute (NFI) has a great deal of in-house knowledge in the field of forensic products, research and services, and provides many organizations in the field of security and law with reliable information from traces. Think, for example, of biological, chemical, digital or physical traces at a crime scene. Mathematical models are used within the NFI to understand the evidential value of the traces found.
Marjan Sjerps has been working at the NFI since 1993. When Marjan started there were no other statisticians at the NFI, she was the first forensic statistician in the Netherlands! Marjan is currently a member of a team of about twenty experts who are researching the applications of machine learning, statistics and probability in forensic science and criminal justice. This involves interpreting evidence, whereby evidential value is expressed in a ratio of two probabilities. Since 2010, Marjan has also been professor by special appointment for forensic statistics at the University of Amsterdam, an appointment with the aim of further strengthening the collaboration between the NFI and the university.

“I started out as a mathematician, graduating in statistics and operations research in Nijmegen. After my studies I decided to do a PhD. I ended up at the institute for theoretical biology in Leiden. That was a lot of fun and I learned a lot, but I knew I didn't want to dedicate my life to this. After my PhD I started searching and saw a vacancy at the NFI in the newspaper. They were looking for someone with knowledge of statistics but also population genetics, this was related to my PhD topic. That is how I became the first forensic statistician in the Netherlands.”
Within the NFI, Marjan mainly conducts research into methods for calculating the evidential value of (a combination of) observations by forensic investigators. The observations can come from all kinds of forensics, but the method itself is generally applicable. Recently, for example, this method was applied to a dataset of digital traces found on mobile telephones, and a dataset of torn pieces of duct tape.
A detective called Bayes
To explain this general method, forensic DNA-testing is a good example. By means of statistical models it is possible to say something about how likely it is that a trace that has been found comes from a specific suspect. Central to the forensic investigation within the NFI is Bayes' rule, which reads as follows:
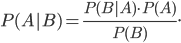
In the formula, 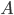 and
and 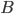 stand for events,
stand for events, 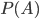 (
(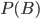 respectively) stands for the probability that event
respectively) stands for the probability that event 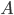 (
(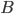 respectively) will happen, and
respectively) will happen, and 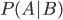 that event
that event 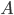 will happen given that
will happen given that 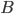 happens. Mathematicians call such probabilities conditional probabilities. How is Bayes' rule used in forensics?
happens. Mathematicians call such probabilities conditional probabilities. How is Bayes' rule used in forensics?
Suppose a crime has been committed and DNA traces have been found at the crime scene. Then the NFI will use these traces to make a DNA profile that may belong to the perpetrator. The DNA profile created can then be compared with the DNA profiles in the (inter)national DNA databases. Suppose there is a match with a profile from the databases. Then this person can be designated as a suspect. Now the NFI needs to evaluate this match. This is where Bayes' rule comes in play. The prosecution argues that hypothesis 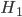 is true, namely that the DNA trace comes from the suspect, the defence argues that the alternative hypothesis
is true, namely that the DNA trace comes from the suspect, the defence argues that the alternative hypothesis 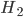 is true, namely that the DNA trace does not come from the suspect. Applying Bayes' rule then yields
is true, namely that the DNA trace does not come from the suspect. Applying Bayes' rule then yields
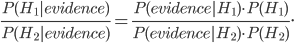
The quotient on the left is the ratio between the probabilities of the two hypotheses given the evidence, this is called the posterior odds. The middle factor is called the likelihood ratio and the factor on the far right is called the prior odds, the ratio between the probabilities of the two hypotheses before considering the evidence.
The crux of the statistical analysis lies in determining the likelihood ratio. A likelihood ratio of less than one means that the evidence is beneficial to the suspect, on the other hand, a likelihood ratio greater than one means that the evidence is detrimental to the suspect. The conclusion that is ultimately submitted to the court indicates to what extent the collected evidence fits better with one hypothesis than with another. An example of how the conclusion is formulated is roughly as follows: the findings of the DNA test are approximately 100,000 times more likely if the cell material in the sample comes from the suspect than if the cell material in the sample comes from a random unknown person. The judge then takes the conclusions of the forensic investigation into account when determining the verdict.
“We first create a forensic DNA profile, which reveals certain parts of the DNA that we know can differ between individuals in a population. Then we can search the databases to find a match. When a match is found, experts are done in television series such as CSI, but in real life it becomes interesting at this point: the crucial question is what the evidential value of that match is. Bayes' rule is very central to forensic research and makes it possible to draw conclusions even with DNA traces that are mixed or severely damaged, for example half eaten by bacteria. We use advanced software to calculate a likelihood ratio. An aspect that we always take into account is that a DNA match can occur by chance. How often the observed DNA features occur in the population plays a role in determining the likelihood ratio. In addition to the question "whose DNA is this?", the question “how did the DNA get there?” becomes more and more important. Other aspects play a role in the likelihood ratio, such as the probability that DNA will be transferred during certain activities.”
Within the NFI there is a lot of interaction between mathematicians, chemists, biologists, computer scientists and medical doctors, but also sometimes with the police and lawyers. “I really enjoy working in such a diverse team. For example, I am sometimes called upon to present our conclusions in a court of law. I also really enjoy working one day a week at the university, with mathematicians and with the other colleagues from the master forensic science. They have a certain way of thinking and I find that interesting. The diversity and depth of my work ensures that I am never bored and that is what I love about it.”
This interview is a translation of the original interview written for Pythagoras (in Dutch) together with Annelene Schulze. Featured image is by the photo archive of the NFI.