A mathematical overview of 2018!

Some memorable moments for mathematics from last year, both on a global level but also within the Networks program!

The Abel prize

The mathematician Robert Langlands (Princeton) was awarded the prestigious Abel prize. In 1967 Langlands, he was then a university teacher at Princeton, sent a letter with his findings to the mathematician André Weil. In his letter he described a revolutionary theory making deep connections between number theory and harmonic analysis. These two areas of mathematics were considered until then as unbridgeable. His innovative ideas have lead to the Langlands program, a web of far-reaching and influential conjectures about connections between these two fields of mathematics.

Robert Langlands

Fields, Nevanlinna and Leelavati

It was the year the prestigious Fields medal was awarded. The Fields medal is awarded to two, three, or four mathematicians under 40 years of age at the International Congress of the International Mathematical Union (IMU), a meeting that takes place every four years. On August the 1st, in a conference hall in Rio de Janeiro four names were announced, Caucher Birkar (Cambridge), Alessio Figalli (ETH), Peter Scholze (Bonn) and Akshay Venkatesh (Stanford). Birkar does research in algebraic geometry, Figalli is an expert in optimal transport, which he applies to partial differential equations, geometry and probability theory. Scholze has made major contributions in algebraic geometry and representation theory. Venkatesh explores the connections between analytical number theory, dynamics, topology and representation theory.

From top left to bottom right, Caucher Birkar, Alessio Figalli, Peter Scholze and Akshay Venkatesh.

While the Fields medal may attract most of the attention, there are two more prizes awarded during the International Congress of the IMU, the Rolf Nevanlinna Prize and the Leelavati Prize. The Rolf Nevanlinna Prize is awarded for outstanding contributions in Mathematical Aspects of Information Sciences, last year awarded to Constantinos Daskalakis (MIT). The award cites his “powerful body of results” that explicate core questions in economics about how rational players behave in games and markets, as well as his more recent work in machine learning.

Constantinos Daskalakis

The Leelavati Prize is intended to accord high recognition of outstanding contributions for increasing public awareness of mathematics as an intellectual discipline and the crucial role it plays in diverse human endeavors. Last year the Leelavati Prize was awarded to Ali Nesin (Istanbul), for his outstanding contributions towards increasing public awareness of mathematics in Turkey, in particular for his tireless work in creating the "Mathematical Village" as an exceptional, peaceful place for education, research and the exploration of mathematics for anyone.

Ali Nesin

The Nesin Mathematics Village

The Hadwiger-Nelson problem

In 1950 Edward Nelson, asked the kind of deceptively simple question that can give mathematicians fits for decades. Imagine, he said, a graph — a collection of points connected by lines. Ensure that all of the lines are exactly the same length, and that everything lies on the plane. Now color all the points, ensuring that no two connected points have the same color. Nelson asked: What is the smallest number of colors that you’d need to color any such graph, even one formed by linking an infinite number of vertices?

The problem, now known as the Hadwiger-Nelson problem or the problem of finding the chromatic number of the plane, has piqued the interest of many mathematicians, including the famously prolific Paul Erdős. Researchers quickly narrowed the possibilities down, finding that the infinite graph can be colored by no fewer than four (William en Leo Moser, 1961) and no more than seven colors (John R, Isbell). But it is sometimes that major mathematical breakthroughs don't come from inside the mathematical community! But from people doing mathematics for the fun of it! It was in April that Aubrey de Grey, a British biomedical gerontologist and bio-informatician, raised the lower bound from four to five colors! He constructed a graph with 1.581 points which can't be colored only with four colors. The Dutch mathematician Marijn Heule (Austin), managed then to reduce the size of the graph first to 826 points, and then to 610 points! In order to construct his graph Heule used SAT-solvers. Who knows what will happen in 2019 regarding this problem!

The 826-graph that Marijn Heule constructed.

Breakthrough in Quantum Computing

During 2018 a major breakthrough occurred in the area of quantum computers and quantum algorithms. A question that computer scientists posed in 1993 was the following: "Are there problems that only a quantum computer can solve, while a classical computer would fail?". It was in 2018 this question was answered!

Photo taken from nanalyze.com

Two computer scientists, Ran Raz (Princeton) and Avishay Tal (Stanford) published on May 31st an article where they proved that such a problem indeed exists.

The problem goes as follows, suppose you have two random number generators and each one of them generates a sequence of numbers. Is it then possible for a computer to determine If these two sequences are completely independent of each other? a quantum computer can solve this problem with only one hint. A classical computer, no matter how advanced, can't answer this question even if we provide it with infinitely many hints. Hence Raz and Tal proved that the class of problems a quantum computer can solve, denoted by BQP, is fundamentally different from the class of problems a classical computer can solve, denoted by PH.

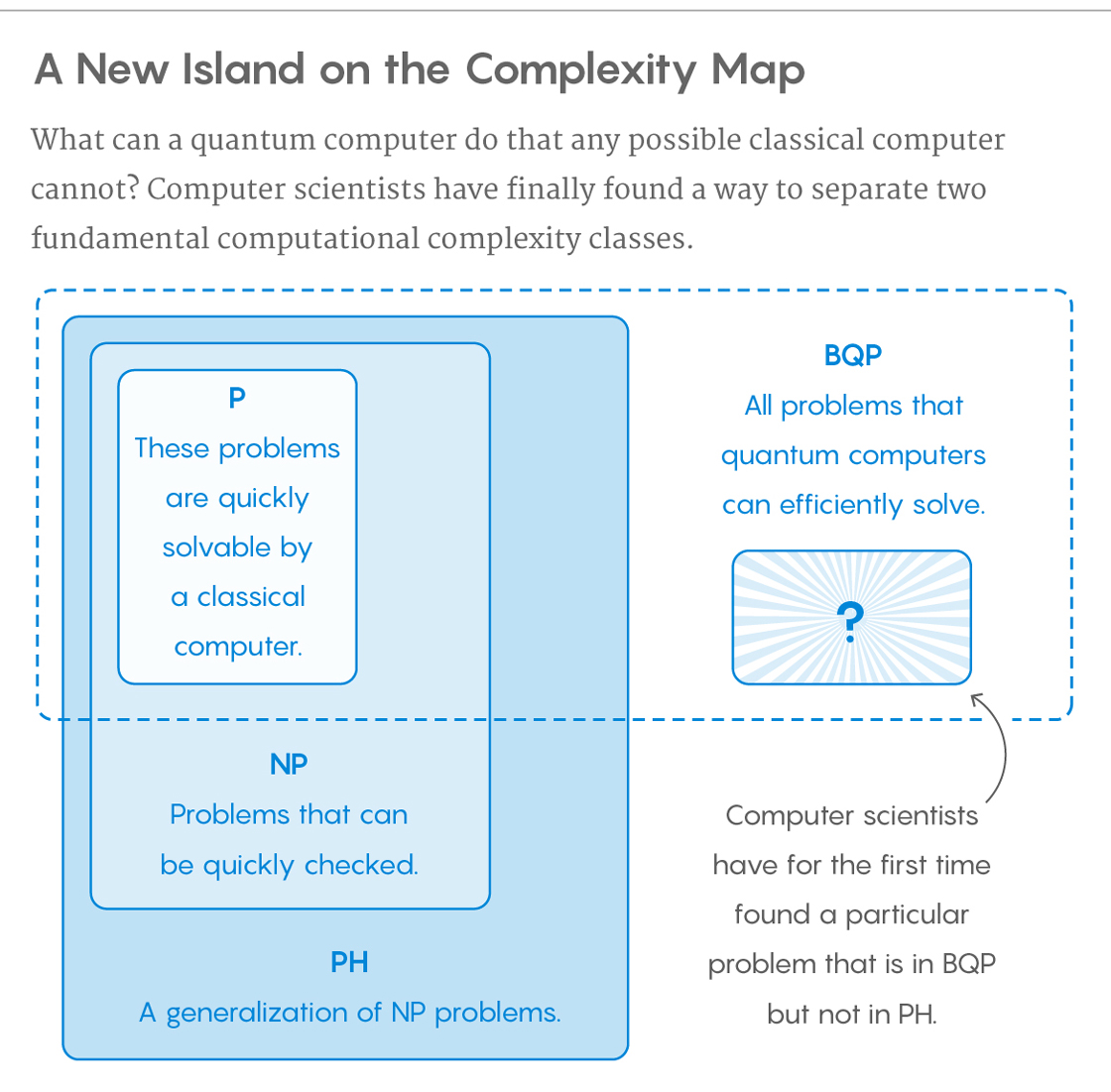
Photo taken from quantamagazine [5].

A theorem in Japan, a conjecture in the rest of the world

In the report "Why abc is still a conjecture", Fields medal winner Peter Scholze (Bonn) and Jakob Stix (Frankfurt) describe a “serious, unfixable gap” within a mammoth series of papers by Shinichi Mochizuki, a mathematician at Kyoto University who is renowned for his brilliance. Posted online in 2012, Mochizuki’s papers supposedly prove the abc conjecture, one of the most far-reaching problems in number theory [7].

Despite multiple conferences dedicated to explicating Mochizuki’s proof, number theorists have struggled to come to grips with its underlying ideas. His series of papers, which total more than 500 pages, are written in an impenetrable style, and refer back to a further 500 pages or so of previous work by Mochizuki, making it extremely difficult for the mathematical community to follow. Consequently, only mathematicians in “Mochizuki’s orbit” have vouched for the proof’s correctness. “There is nobody else out there who has been willing to say even off the record that they are confident the proof is complete.” [7]

Nevertheless, wrote Frank Calegari of the University of Chicago in a December blog post, “mathematicians are very loath to claim that there is a problem with Mochizuki’s argument because they can’t point to any definitive error.” But apparently Mochizuki's papers now been accepted by the Publications of the RIMS (a journal where Mochizuki himself is the managing editor) which led to the controversial situation of a statement being a theorem, the abc- theorem, in Japan and a conjecture in the rest of the world. That has now changed. In their report, Scholze and Stix argue that a line of reasoning near the end of the proof of “Corollary 3.12” in Mochizuki’s third of four papers is fundamentally flawed. The corollary is central to Mochizuki’s proposed abc proof. Let's see how the discussions will go in 2019!

NETWORKS

Within the NETWORKS program there were also some memorable events that took place!

The first doctorates

August 28^th was a special day for NETWORKS since the very first NETWORKS PhD students defended their PhD theses. Souvik Dhara and Debankur Mukherjee not only graduated on the same day, but also both received the cum laude distinction. Souvik Dhara received the cum laude distinction for his PhD thesis entitled “Critical Percolation on Random Graphs with Prescribed Degree Sequences”. The thesis gives an impressively complete description of the possible behaviors of critical percolation on random graphs, in which the degree sequence is fixed. Debankur Mukherjee received the cum laude distinction for his PhD thesis entitled "Scalable Load Balancing in Networked Systems". The thesis contains a stunning collection of groundbreaking results at the frontier of a booming and highly competitive domain of research. Debankur has in particular pioneered the notion of asymptotic optimality and universality of load balancing algorithms, as an overarching perspective on scalability issues in large-scale data centers.

Debankur and Souvik!

On the 5th of December Andrea Roccaverde defended his PhD thesis in Leiden. In his thesis, entitled "Breaking of ensemble equivalence for complex networks", Andrea studied the phenomenon of breaking of ensemble equivalence. For many systems in statistical physics the microcanonical and canonical ensemble are equivalent in the thermodynamic limit, but not for all. The goal of Andrea's research was to classify for which classes of complex networks with topological constraints, breaking of ensemble equivalence occurs.

Andrea receiving his doctorate

Congratulations Andrea, Debankur and Souvik!

The Dutch Academy of Sciences and grants

On the 19th of April the Dutch Academy of Sciences announced that Prof. Remco van der Hofstad (TuE) and Prof. Monique Laurent (CWI) were selected as new members of the Academy. The Academy has approximately 550 members. Membership is awarded on the basis of scientific and scholarly achievement.

Various people affiliated with Networks were also successful in the grant proposals they submitted. All of them are mentioned on the Networks website. Congratulations to all of you for the amazing research you do!

The KWG PhD-prize

Six PhD students get the opportunity every year to present their work during the Dutch Mathematical Congress (NMC). Last year, Clara Stegehuis was one of the nominees who held a presentation about their research during the congress. Her presentation on networks and epidemics convinced the jury to choose her as this year’s winner of the KWG PhD prize. An important criterion for winning the award was the PhD candidate’s ability to make the subject accessible to non-specialists. Therefore the presentation had to be aimed at a general mathematical audience. A requirement Stegehuis is familiar with, since she is one of the Faces of Science bloggers.

Clara receiving the PhD-prize from Peter van Emde Boas and Jan Wiegerinck

Masterclass

On 18 and 23 April 2018 a masterclass event on networks and their applications was organized by the NETWORKS program at Leiden University and the University of Amsterdam. This two day event was intended for secondary education students and teachers. About 25 students participated in the event which was praised as a big success by the teachers and the students!