Last month I was back in the classroom. But this time the kiddos in my class were quite younger than I'm used to: instead of a class of university students, this time I had an enthusiastic group of school students in front of me.
In action on the board during the masterclass.
The subject was also different from what I am used to: normally I help with the introductory university course in probability theory for the study of mathematics, but this time I was allowed to talk about the specific subject of my own research.
The lessons I prepared were part of the NETWORKS goes to school program, for which two masterclasses on network-related topics are organized annually. The first masterclass was about the Dijkstra algorithm, the algorithm that your navigation (e.g. Google Maps) uses to find the shortest route to your destination. The second masterclass was about community detection: detecting groups in networks, such as groups of friends in social networks or topics from Wikipedia pages (see picture below). I prepared and gave this second masterclass.
The network of network-related Wikipedia pages. Each dot is a Wikipedia page, and two pages are connected when one references the other. When you apply community detection to this network, you see that the pages are roughly classified by subject (for example, social networks and the World Wide Web). Image taken from Medium.com.
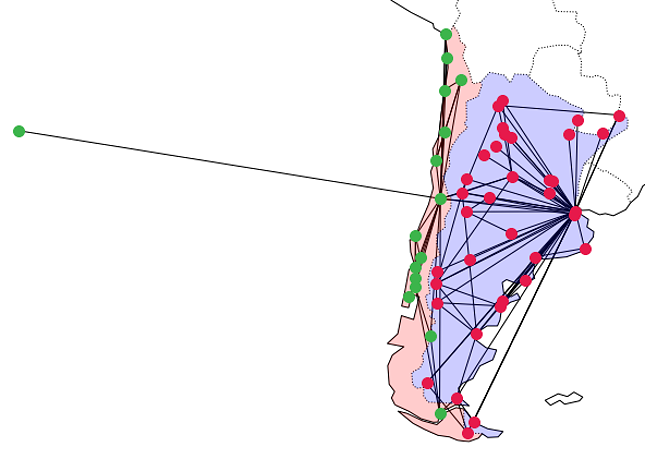
During the masterclass I gave a short introduction to community detection. I explained different algorithms and gave examples of small networks on which you can try these algorithms, such as the network of airports and the network of last year's football World Cup (see pictures below). The material of the two masterclasses can be found here.
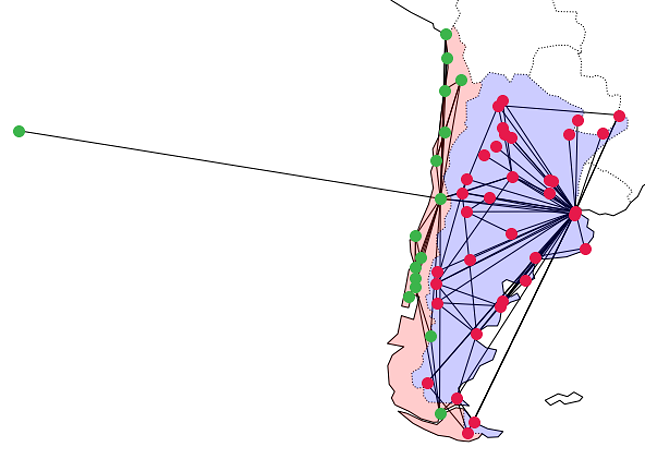
The network of airports in Chile and Argentina. Can an algorithm recognize which airport belongs to which country based on the network alone? (and not the locations or names of the airports).
It was very nice to see that the students were so interested. I was also very surprised that they picked it up so quickly! For me, it has also been almost ten years since I was in high school, and I had completely forgotten what I found difficult and what not. Of course, in the ten years that I have been involved in mathematics, there are many things that I used to find very difficult, but nowadays I hardly have to think about them.
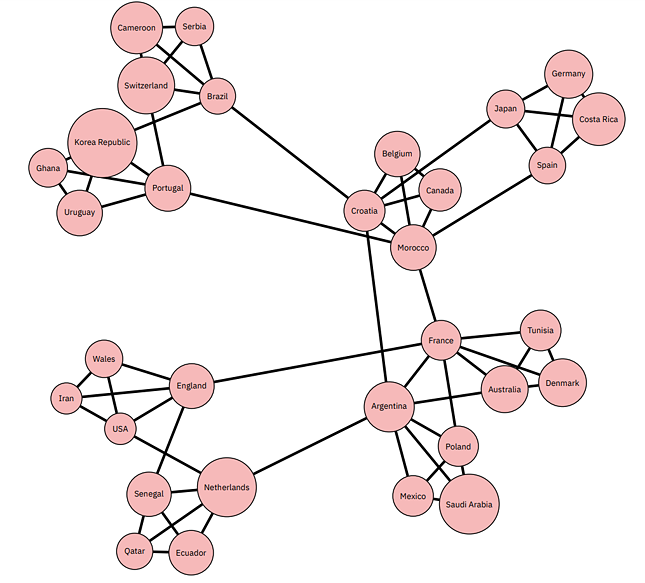
The network of last year's World Cup football. Two teams are linked when they have played a match against each other. In this network you can clearly see the division into groups.
For example, I noticed that the students found it easier to work with numbers than with x's and y's, while I find it easier the other way around. Because you actually do exactly the same thing, but when you enter numbers you actually have to do the arithmetic, and we mathematicians find that difficult. I really enjoyed showing that there is a lot more math than what you get in high school. When I started my math studies, I noticed that the math I learned here is very different from the math I was taught in high school.
In secondary school, you mainly receive instructions on how to perform certain calculations. While math in college is more like a puzzle where there is no clear step-by-step plan towards the answer, but you have to use your creativity to solve problems. Hopefully I was able to give the students a nice taste of this puzzle!
This post is a traslation of Martijn's original blog post written for Faces of Science for Kennislink!
If, after reading the title, your immediate response is to shout "1/6-th", then you have correctly answered the question. Well done! However, in this article we will focus on the meaning of this question. What exactly is this "chance" of which you've just exclaimed it equals 1/6-th?
In November 2024 a masterclass on networks and algorithms will be organised by the mathematics research program NETWORKS. Teachers and school students at the level of VWO 5-6 are welcome to join this two-day masterclass, no specific prior knowledge is needed, only enthousiasm about mathematics!
Have you ever wondered what kind of insights you can gain about games by looking at it using a mathematical lens? In this article we have a look at Snakes and Ladders, and in a follow up article we will dive into Monopoly!
