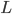In the interactive simulation below, developed by Martijn Gosgens, you can see how the two-community Kuramoto model works.
In the simulation you are able to adjust a variety of parameters of the model before starting the simulation and seeing what happens. The first parameters you can adjust are the number of nodes (colored dots) in each community. 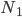 represents the number of nodes in the red community and
represents the number of nodes in the red community and 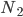 the number of nodes in the green community. Next you are able to adjust the strength with which red nodes attract other red nodes (
the number of nodes in the green community. Next you are able to adjust the strength with which red nodes attract other red nodes (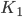 ) and the strength with which green nodes attract other green nodes (
) and the strength with which green nodes attract other green nodes (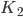 ). We are predominantly interested in cases where both
). We are predominantly interested in cases where both 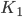 and
and 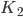 are positive (but feel free to experiment with negative, i.e. repulsive,
are positive (but feel free to experiment with negative, i.e. repulsive, 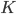 ’s). The parameters
’s). The parameters 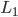 and
and 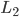 are the strength with which red nodes are attracted (or repulsed) by green nodes and the strength with which green nodes are attracted by red nodes respectively. When these are positive the interaction between the two communities is attractive, when they are negative the interaction is repulsive. The last model parameter you can adjust is the noise strength,
are the strength with which red nodes are attracted (or repulsed) by green nodes and the strength with which green nodes are attracted by red nodes respectively. When these are positive the interaction between the two communities is attractive, when they are negative the interaction is repulsive. The last model parameter you can adjust is the noise strength, 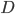 . This should be greater than or equal to zero and it adjusts the amount that the nodes jiggle. Making
. This should be greater than or equal to zero and it adjusts the amount that the nodes jiggle. Making 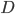 larger makes the nodes jiggle more.
larger makes the nodes jiggle more.
In the next bit of the simulation you can adjust how the dots will be placed on the circle initially (when the simulation starts) as well as the natural properties of the oscillators. With the “Frequencies” option you can select “constant zero” or “standard normal”. Selecting “constant zero” gives each dot the property that it would stand still if there where no other dots and selecting “standard normal” gives each dot its own speed it would rotate around the circle with (drawn from a normal distribution). Finally, you can change how the dots start on the circle. The initial positions are taken randomly from two (normal) distributions. By changing 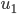 and
and 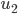 you adjust the mean of these distributions and by adjusting the slider for
you adjust the mean of these distributions and by adjusting the slider for 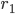 and
and 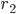 you adjust how peaked (concentrated) the distribution is.
you adjust how peaked (concentrated) the distribution is.
Let’s consider an example: We will set the number of nodes to 200 per community. We will set both 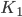 and
and 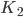 to 5, both
to 5, both 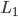 and
and 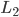 to -2 and
to -2 and 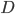 to 1. Next we take the Frequencies to be “constant zero”, set both
to 1. Next we take the Frequencies to be “constant zero”, set both 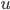 ’s to 0 and both
’s to 0 and both 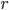 ’s to 0.75. This means that the nodes will initially be fairly concentrated (an
’s to 0.75. This means that the nodes will initially be fairly concentrated (an 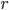 of 1 would be that they are all on the same spot, while 0 is completely spread out on the circle) around the zero point on the circle (the right most point on the circle).
of 1 would be that they are all on the same spot, while 0 is completely spread out on the circle) around the zero point on the circle (the right most point on the circle).
Now click on “Restart Simulation” (maybe restart it a couple of times to check if what you see is repeatable). What do you observe? Why? What happens when you change 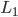 to 2 and
to 2 and 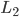 to -3? What do you observe if you choose different values for
to -3? What do you observe if you choose different values for 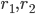 ? Take some time to play around with the simulation.
? Take some time to play around with the simulation.
Click here to have a look at the mathematics behind this simulation!