Let's see how many configurations of the plugboard with k cables are possible. First we have to consider in how many ways we can choose k pairs of letters. Well, this is just
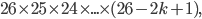
since we have 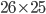 possibilities for the first pair,
possibilities for the first pair, 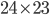 for the second pair, and so on. Finally, we have
for the second pair, and so on. Finally, we have 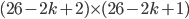 possibilities for the last pair, since a total of
possibilities for the last pair, since a total of 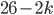 letters are not connected on the plugboard at all. We can write this as a total of
letters are not connected on the plugboard at all. We can write this as a total of 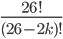 possibilities.
possibilities.
There is, however, a problem with this answer. Let’s say we have a cable connecting letters 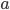 and
and 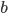 , that would be the same as connecting
, that would be the same as connecting 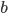 and
and 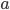 . This means we’re counting the total number of possibilities double for each cable. To account for this, we divide the previous answer by
. This means we’re counting the total number of possibilities double for each cable. To account for this, we divide the previous answer by 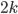 .
.
We’re not finished yet, though. Let’s say we have plugged up the plugboard with 11 cables. Then there are 4 letters which are not connected to another letter on the plugboard, let’s say 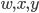 and
and 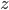 are not connected. Well, that would be the same configuration if we hadn’t connected
are not connected. Well, that would be the same configuration if we hadn’t connected 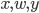 and
and 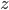 , since the cables are still connected the same. But in our previous answer these configurations are counted separately. To account for this, we divide by the number of ways we can arrange
, since the cables are still connected the same. But in our previous answer these configurations are counted separately. To account for this, we divide by the number of ways we can arrange 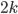 letters, which is
letters, which is 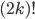 . All in all the total number of possibilities to connect a plugboard with
. All in all the total number of possibilities to connect a plugboard with 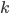 cables is equal to:
cables is equal to:
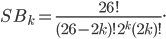
We can now calculate for 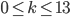 in how many ways we can configure the plugboard:
in how many ways we can configure the plugboard:
We see that if we use a total of 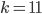 cables, the total number of plugboard configurations is the highest, i.e. the safest option to use. This is interesting, since up until 1938, the Germans used six cables. Seven or eight cables were used after 1938, and it was not until 1943 that the Germans finally used the safest option of ten cables.
cables, the total number of plugboard configurations is the highest, i.e. the safest option to use. This is interesting, since up until 1938, the Germans used six cables. Seven or eight cables were used after 1938, and it was not until 1943 that the Germans finally used the safest option of ten cables.
