Vaak zijn er meerdere strategieën denkbaar om een bepaalde taak uit te voeren – ofwel om "een bepaald probleem op te lossen", zoals het meestal wordt genoemd – met verschillende algoritmes tot gevolg. Deze algoritmes verschillen normaliter in hoe efficiënt ze zijn: sommige zijn snel, andere langzaam. Natuurlijk hangt de tijd die een computer daadwerkelijk nodig heeft om een probleem op te lossen af van de snelheid van de computer. Sterker nog, het hangt af van de schaal van het op te lossen probleem: duizend getallen op volgorde zetten kost minder tijd dan een miljoen getallen. Toch is het mogelijk om de efficiënties van algoritmes op wiskundige wijze met elkaar te vergelijken. Hiertoe wordt het aantal "stappen" van het algoritme geanalyseerd als functie van het aantal inputelementen.
Neem bijvoorbeeld het algoritme beschreven in Basisbegrippen - Algoritmes om genummerde kaarten op volgorde op te stapelen. Stel de input bestaat uit 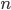 kaarten. Om de kaart met het laagste nummer te vinden, kijken we naar alle n kaarten; om de kaart met het op-een-na laagste nummer te vinden naar
kaarten. Om de kaart met het laagste nummer te vinden, kijken we naar alle n kaarten; om de kaart met het op-een-na laagste nummer te vinden naar 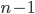 kaarten, enzovoorts. In totaal doorlopen we dus
kaarten, enzovoorts. In totaal doorlopen we dus 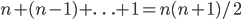 stappen. Ook al hangt het precieze aantal af van wat we als "stap" beschouwen, wat belangrijk is, is dat het aantal stappen kwadratisch toeneemt met het aantal kaarten dat gesorteerd moet worden. In technische bewoordingen is de looptijd van het algoritme
stappen. Ook al hangt het precieze aantal af van wat we als "stap" beschouwen, wat belangrijk is, is dat het aantal stappen kwadratisch toeneemt met het aantal kaarten dat gesorteerd moet worden. In technische bewoordingen is de looptijd van het algoritme 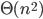 . Als de looptijd van een algoritme kwadratisch toeneemt, duurt het vier keer langer als de input verdubbelt. Een algoritme waarvan de looptijd lineair toeneemt – we schrijven: de looptijd is
. Als de looptijd van een algoritme kwadratisch toeneemt, duurt het vier keer langer als de input verdubbelt. Een algoritme waarvan de looptijd lineair toeneemt – we schrijven: de looptijd is 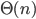 – kost maar twee keer zoveel tijd als de input verdubbelt. Lineaire-looptijdalgoritmes zijn dus veel sneller dan kwadratische-looptijdalgoritmes bij grote inputs.
– kost maar twee keer zoveel tijd als de input verdubbelt. Lineaire-looptijdalgoritmes zijn dus veel sneller dan kwadratische-looptijdalgoritmes bij grote inputs.
Een belangrijk onderscheid tussen algoritmes is of hun looptijd polynomiaal toeneemt met de inputschaal 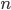 , bijvoorbeeld als
, bijvoorbeeld als 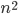 of
of 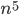 , of exponentieel, als
, of exponentieel, als 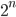 of
of 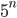 . De looptijd van laatstgenoemde type algoritmes groeit zo snel dat ze in feite onbruikbaar zijn tenzij de inputschaal zeer klein is. Stel, bijvoorbeeld, dat we een algoritme hebben dat
. De looptijd van laatstgenoemde type algoritmes groeit zo snel dat ze in feite onbruikbaar zijn tenzij de inputschaal zeer klein is. Stel, bijvoorbeeld, dat we een algoritme hebben dat 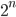 stappen uitvoert bij een inputschaal
stappen uitvoert bij een inputschaal 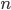 , en dat we een computer hebben die 1 miljard stappen per seconde kan uitvoeren. In dat geval kost het het algoritme ongeveer 1 seconde bij een input van 30. Maar als de inputschaal 50 is, zou het 36 jaar kosten... Het helpt niet veel om een snellere computer te kopen. In plaats daarvan zou je moeten proberen om een efficiënter algoritme te bedenken. Het zoeken naar het efficiëntste algoritme voor een bepaald rekenprobleem is een levendige en belangrijke tak van sport binnen de theoretische informatica.
, en dat we een computer hebben die 1 miljard stappen per seconde kan uitvoeren. In dat geval kost het het algoritme ongeveer 1 seconde bij een input van 30. Maar als de inputschaal 50 is, zou het 36 jaar kosten... Het helpt niet veel om een snellere computer te kopen. In plaats daarvan zou je moeten proberen om een efficiënter algoritme te bedenken. Het zoeken naar het efficiëntste algoritme voor een bepaald rekenprobleem is een levendige en belangrijke tak van sport binnen de theoretische informatica.
