Most people, when asked about mathematics will (unfortunately) say it’s dull at best. Yet when you ask mathematicians what they like most about the job, their answer will very likely be the exact opposite: mathematicians think that they have one of the most fulfilling and creative jobs in the world!
This is not just propaganda, it is backed up by facts: Careercast makes an annual list of the best jobs to have, and as every year, math-related jobs crowd the top ten. Last year, Data Scientist was #1, Statistician #3, Research mathematician #6, and Actuary #10!
So what explains this complete dissonance between what most people think about maths, and what professionals think? It probably has to do with high-school: Although high-school math has become a lot more compelling in the past decades, it is still a simple fact that the learning curve of mathematics is steep. Almost everyone struggles with those first years, and struggling is not fun.
But once you master those “basics”, mathematics does get really fun. Unfortunately, there are so many basics that this usually only happens at university.
Yet there are plenty of fun mathematics problems that you can tackle with just a bit of cleverness. The excellent blog Futility Closet publishes such problems with high frequency. To give you a sense of what research mathematics is like, you could try your hand at a few. The puzzles I’ve selected here are all networks related (some more obviously than others). It is really worth stressing that the kind of thinking that goes into solving these puzzles is exactly at the core of what research mathematicians do. Which explains why mathematicians like their jobs so much!
Good luck with the puzzles! (The solutions can be found on Futility Closet. Just follow the links.)
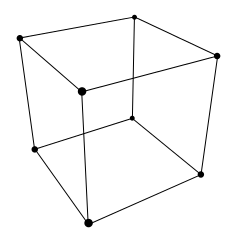
You’re planning to make the wire skeleton of a cube by arranging 12 equal lengths of wire as shown and soldering them at the corners.
It occurs to you that you might be able to simplify the job by using one or more longer lengths of wire and bending them into right angles at the cube’s corners.
If you adopt that plan, what’s the smallest number of corners where soldering will still be necessary?
Each cell in an 8×8 grid contains an arrow that points up, down, left, or right. There’s an exit at the top edge of the top right square. You begin in the bottom left square. On each turn, you move one square in the direction of the arrow, and then the square you have departed turns 90° clockwise. If you’re not able to move because the edge of the board blocks your path, then you remain on the square and it turns 90° clockwise. Prove that eventually you’ll leave the maze.
A city has 10 bus routes. Is it possible to arrange the routes and bus stops so that if one route is closed it’s still possible to get from any one stop to any other (possibly changing buses along the way), but if any two routes are closed, there will be at least two stops that become inaccessible to one another?
An odd number of people armed with water guns are standing in a field so that all the pairwise distances are distinct. At a signal, each shoots at his nearest neighbor and hits him. Prove that one person doesn’t get wet.
In this article, we will discuss a mathematical riddle that "seems impossible even if you know the answer". It is better known as the 100 prisoners problem.
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
Since 2016 the world has been witnessing the Rohingya genocide in Myanmar, in 2021 we all saw the Capitol riots on tv. What do networks have to do with these events?
Have you ever found yourself less popular when compared to your friends? Interestingly, in any group of individuals, on average, people have fewer friends than their friends do, or at the very most, an equal number. Not more!
We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
