The moment millions of fans have waited for is there: the finale of Game of Thrones. 75 characters in different parts of the world, fighting to be the ruler of the iron throne. But who is the mathematical ruler of the iron throne?
Game of Thrones is the most popular tv series of recent times. The complexity of the show is incomparable to any other popular film or tv series: season one already contained 127 characters. Because of the short life span of the characters, ‘only’ 75 remain in the final season. The characters live in different parts of the world, and who the protagonists are changes with the season (usually because a character dies).
To compare: the eight Harry Potter films have three protagonists, who mostly stay together. The four protagonists of Desperate Housewives live in the same street for eight seasons. In short, keeping up with Game of Thrones is a real challenge for your brain! This challenge is nice of course, but it does not make the show easier to follow. Who, out of all characters, is the real protagonist? Every fan probably has his or her own opinion, but it would be nice to end this discussion once and for all by using objective arguments.
A network of characters
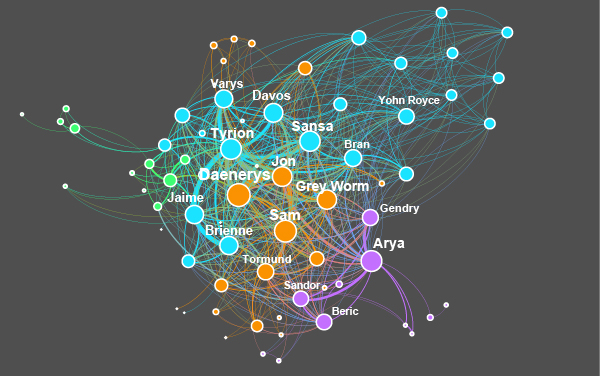
Luckily, network science can help us out here! You can visualize all connections of characters of the tv show in one network. Every character is a point in the network. A connection between two points can mean two things: either the characters appeared in the same shot, or one character talked about the other one. Characters who are long dead can also appear in the network in this way, as long as sufficiently many people talk about them.
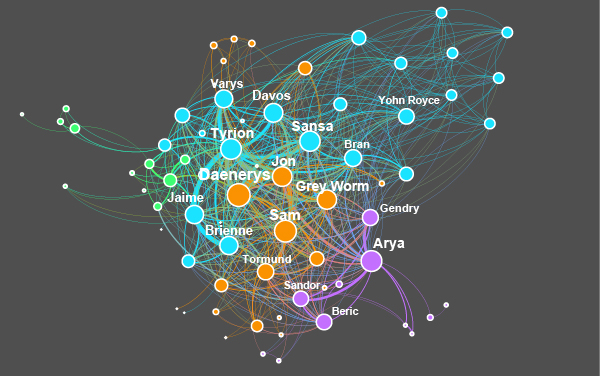
Figure 1: You can visualize all connections of characters of the tv show in one network.
Who are your connections?
We use this network to find out who the real protagonist of Game of Thrones is. On first sight, we can achieve this by counting who has the most connections. Sam, member of the Night Watch, then ends up in the first place.
But wait a minute: not all connections are equally important if you want to find out how much influence a character has, and therefore how important the character is to the story. You create more influence when you befriend a king then when you befriend a beggar. Also, your influence probably increases less when you befriend a person who already has a thousand friends, than when you befriend someone who does not know many people.
Google and Game of Thrones
Interestingly, this is the same conclusion that made Google successful in 1990. Larry Page and Sergey Brim were looking for a method to determine how high your webpage should appear in the search results. When an important webpage links to yours, your webpage ends up higher in the results. But if this webpage also links to a thousand other webpages, this makes your webpage less special, and you appear lower in the search results. By applying this so-called PageRank method to rank web pages, Google beat all competitors in the search engine competition.
The same PageRank method can also compute who the most important character is in Game of Thrones. Now the method does not rank important webpages on the internet. Instead, it ranks the most important characters in the Game of Thrones network and we call the algorithm CharacterRank. CharacterRank studies all connections of a character. The higher the CharacterRank score of the connection, the more it increases the CharacterRank score of the character. On the other hand, a connection with a person with many connections increases your score less than a connection with a person with only a few connections.
But this creates a problem: to compute Tyrion’s CharacterRank is, you have to know the CharacterRank of all his connections. To find those, you have to know the CharacterRanks of their connections (including Tyrion). This seems to be a vicious cycle. Fortunately, you can solve this mathematically. By not computing the score of one character at a time, but instead computing the scores of all characters simultaneously (by using so-called matrix equations), you can obtain the CharacterRank scores of all characters.
And the winner is…
In Figure 1, the size of the character indicates its CharacterRank. Danaerys has the highest score, so mathematically speaking she is the real protagonist! Sam ends in second place, and Arya is third. Catelyn Stark, only mentioned by other characters because of her early death, and Martha, a kitchen girl who spies on Danaerys share the last place. Mathematically speaking, they are the least important in the story.
Early stars
Was Game of Thrones always this complicated? Probably not, if you look at the network of season one. This one is a lot simpler, even though it contained more characters. Danaerys still has her own group of people around her, and does not have many connections with the Stark family for example. Jon is still a watcher on the wall on the outskirts of the world, and he does not have a lot of contact with the rest of the world. Sam, one of the main protagonists of season eight, does not even appear in the network yet.
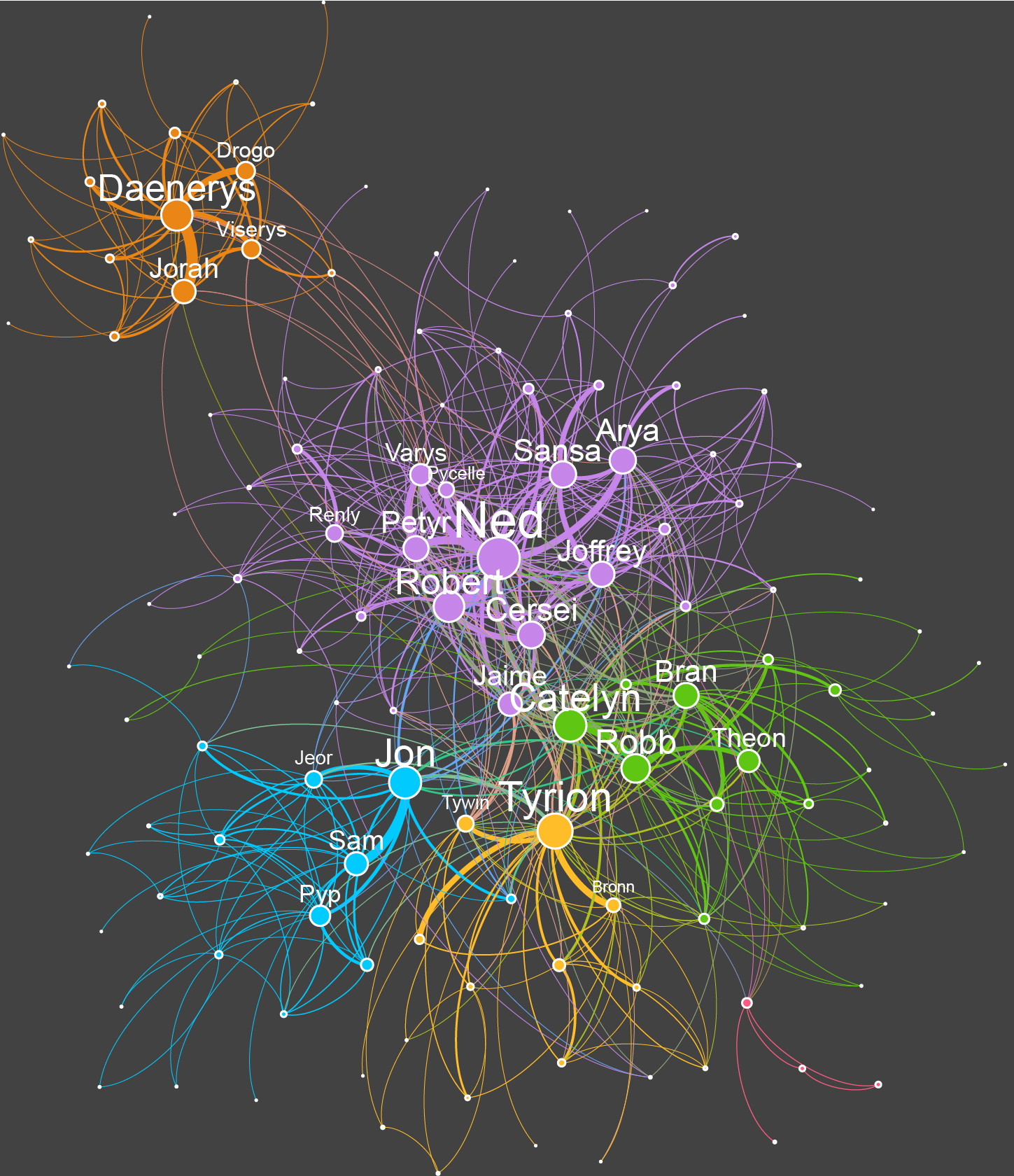
All different groups of characters in the season one network clearly have their own protagonist, but they do not interact much. In season eight this has completely changed: Danaerys and Jon are in the center of the network now. And where Ned was the most important character in season one, he clearly reached his peak too soon: after his death in season one he is still mentioned by other characters, but his importance has clearly ceased.
So mathematically speaking, the best strategy to survive Game of Thrones is to first hide yourself in one of the outskirts of the network. Then you can show yourself in the fights of the later seasons, to become the mathematical ruler of the iron throne.
Recently there has been a breakthrough in the field of algorithms for geometric network problems, concerning the complexity of the Euclidean Travelling Salesman Problem.
If you were born in the previous century, then chances are high that you have spent quite some hours playing Minesweeper, the classic puzzle game that used to be installed on every computer. In this article, we will present a new network-based version of this game and show how network science can help you play this game.
